原论文使用Scala实现:Distributed Minimum Spanning Trees
翻译:分布式最小生成树
MSBD5003 proposal: Proposal: Implementation of MST by pyspark
MSBD5003 final paper:Distributed-MST-pyspark
Github: https://github.com/aszx826477/Distributed-MST-pyspark
项目成员:刘钧元,杨荣锋,尹冬欣,唐慧敏
项目起止:2019年11月2日 - 2019年12月20日
这是MSBD5003: Big Data Computing的团队项目,原论文使用Scala实现的MST最小分布式算法。我们希望用pyspark复现这篇论文中的实验结果,并加深对分布式算法的理解。以下部分是对原论文的翻译,我们复现的论文请查看课程的final paper。
摘要
最小生成树是图论算法中最重要的原型之一。从分类学到图像处理再到计算机网络的众多领域中我们都能找到它们的应用。在此报告中,我们提出了三种算法来计算大型图的最小生成树(MST)或最小生成森林(MSF),这些图不适合单个计算机的内存。在某些假设下,我们分析了这些算法的理论处理时间,通信成本和通信时间。最后,我们使用Apache Spark比较这3种算法对真实数据的性能。该项目的代码可以在这里找到(Scala):https://github.com/s-ramaswamy/CME-323-project
1 介绍
在图论中,连通无回路的无向图称为无向树,简称为树,每个连通分支都是树的无向图称作森林。生成树是无向图导出的子图,且需要包含母图中所有的顶点。最小生成树是所有边的权重总和最小的生成树。
综上所述,最小生成树是连通的、无向的、无回路的、包含原图所有顶点的,且边的权重和最小的生成树。
2 应用领域
最小生成树可以在许多领域中找到应用。下面列出来其中一些。
- 对于NP-hard问题和NP-complete问题,MST是许多近似算法的重要组成部分。例如,对于斯坦纳树(Steiner tree)问题,大多数近似算法的第一步都需要计算MST。这也是Christofede算法中针对旅行商问题的第一步。
- 图像处理中的应用。例如,如果您在幻灯片上有细胞的图像,则可以使用由原子核形成的图的最小生成树来描述这些细胞的排列。
- 它们是单链接聚类的基础。单链接聚类是分层聚类方法。每个元素在开始时都位于其自己的群集中。然后将这些簇依次组合成更大的簇,直到所有元素最终都位于同一簇中。在每个步骤中,将相距最短距离的两个群集组合在一起。稍后我们将看到,此过程基本上模仿了构造MST的Kruskal算法。
- MST的一个明显应用是在道路或电话网络的建设中。我们希望以尽可能短的道路/电线长度连接地方/房屋。这与计算最小生成树完全相同。
3 定理
3.1 切割性质(Cut property)
定理3.1对于图中任意的切割C,如果一条切割边的权重小于其他的切割边,那么这条边一定是该图的最小生成树的边。
证明
下图中,切割将图分为S和V-S两部分,连接两部分有三条边BC、CE和EF,权重分别为6、5、4,假设将边BC划分为最小生成树的一部分,添加边EF会构成环BEFC,反之用BC代替为EF则会产生权重和更小的最小生成树。因此,包含BC的树不是最小生成树。
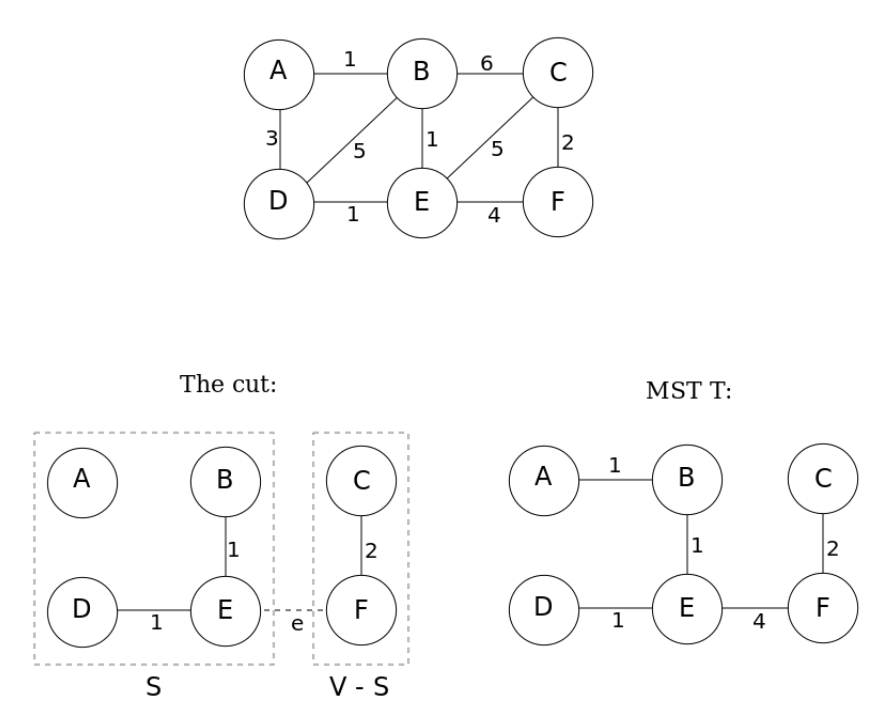
图1图切割性质的示意图
$T$是给定的唯一MST。如果$S = \{ A,B,D,E\}$,则$V - S = \{ C,F\}$,那么跨越切割$(S,V - S)$存在三种可能性,它们是原始图的边BC,EC,EF。其中EF是三条切割边中权重最小的,记为边e,则$S \cup \{ e\}$是MST T的一部分。
3.2 环性质(Cycle property)
定理3.2对于图中任意的环C,如果环中的一条边比其他的任何一条边的权重都大,那么这条边一定不属于MST。
证明
反证法。假设e属于最小生成树$T_{1}$,e是环C中最大的边。删除边e会将$T_{1}$分成两个子树,e的两个顶点分别位于两棵子树上。要想将C重新连接成环,需要构造一条边f,让它的两个顶点分为位于不同的子树上。我们用f重新重新连接C,产生了树$T_{2}$。因为e是环C中最大的边,所以f小于e,故$T_{2}$的权重和小于$T_{1}$,即$T_{1}$不是最小生成树,与原假设矛盾,所以e一定不属于MST。
4 单机算法
4.1 经典算法
单机上最小生成树的两种最受欢迎的算法是Kruskal算法和Prim算法。它们都具有相同的计算复杂度,并且相对容易实现。
4.1.1 Kruskal's算法

G(V,E)中V表示点的集合,E表示边的集合,G表示Graph。Kruskal's算法利用了环性质,即环中最大边一定不属于最小生成树。算法在最开始,需要将所有的边按照由小至大的顺序排列,我们按照这个顺序每次取出一条边,判断是否要加入到MST中。每一轮循环,若该边会构成环则不加入MST,反之则加入MST。因此Kruskal's算法只添加了属于MST的边。
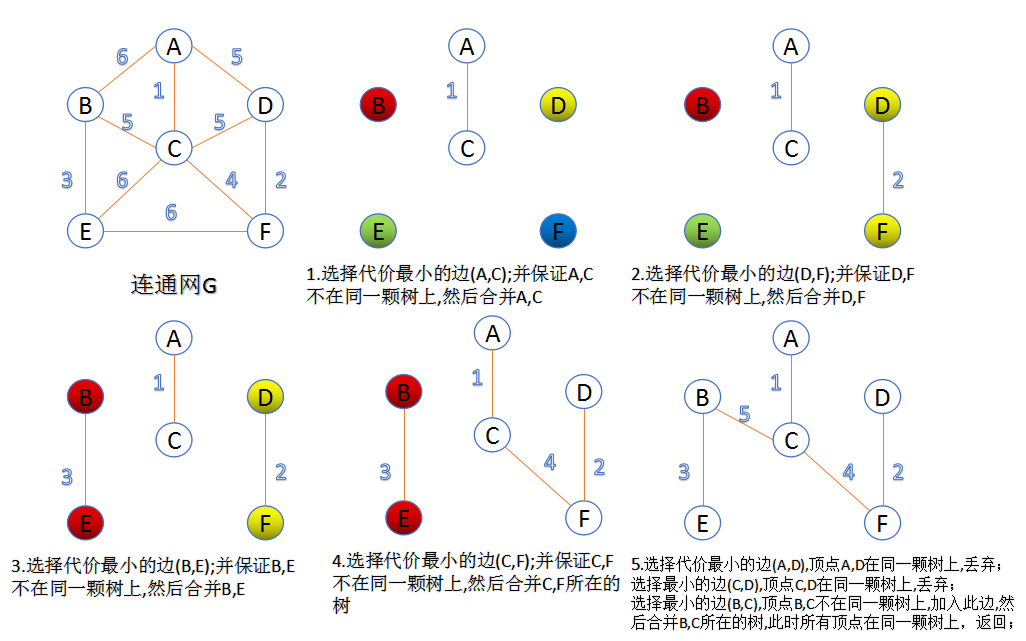
使用不相交的集的数据结构,我们可以实现$O(mlogn)$的时间复杂度,其中m是图的边数,n是图的顶点数。如果我们使用更复杂的不相交集的数据结构,则可以实现$O(m\alpha(m,n))$的时间复杂度,其中$\alpha$是Ackermann函数的反函数,增长及其缓慢。但是要实现此界限,我们需要假设边已经被排好序了,或在线性时间内能完成排序。
4.1.2 Prim's算法

Prim's算法利用切割性质,寻找离开当前树的最小的权重边,并将该边添加到树上。因为切割定理告诉我们,切割边中的最小权重边一定属于MST。所以Prim's算法只添加了属于MST的边。
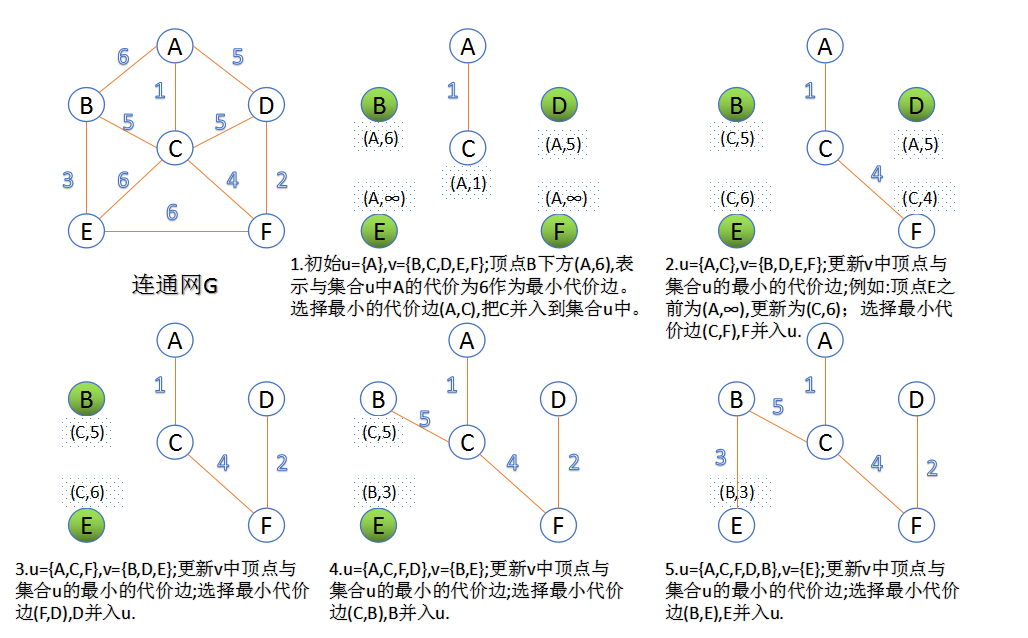
如果我们使用简单的二进制堆(binary heap)和优先级队列(priority queue),则算法的复杂度为$O(mlogn)$,其中m是图的边数,n是图的顶点数。但是,如果我们使用跟复杂的Fibonacci堆,则可能证明算法复杂度为$O(m + nlogn)$,对于稠密图(dense graphs)而言,渐进性更好。
4.2 更快的算法
已知的最快的非随机算法由Bernard Chazelle提出的,它的时间复杂度为$O(m\alpha(m,n))$,实际上就是线性的时间复杂度。但是,该算法使用了软堆(soft heap)和近似的优先级队列,所以难以实现。Karger、Klein和Tarjan发现了一种线性时间的随机算法,该算法仅使用边权重的比较来找到MST。对于整数边权重,目前最快的算法由Fredman和Willard开发,需要$O(m + n)$的时间。
对于本项目,我们仅考虑经典算法,因为它们相对于更快、更新的算法而言,更易于实现。
5 分布式算法
我们将研究三种分布式算法。其中两个基于Kruskal算法——边分割(edge partitioning)和顶点分割(vertex partitioning),第三个是并行Prim's算法(parallel Prim's)。所有这三种算法的基本假设是,图的顶点适合单个计算机的内存,而边则不适合。
首先,我们将研究基于Kruskal的算法。两种算法都有一个共同的主题。以下引理有助于在分布式环境中建立算法的正确性。
引理5.1 子图的MST不包含的边,也不属于原始图的MST。
证明
“子图的MST不包含的边”这个事实表明,在切割中存在另一条权重较小的边,该边将原始边的两个顶点分开。虽然是在子图上考虑这个问题,但实际上对于原始图来说也是如此。因此,子图的MST不会出现的边,也不会出现在原始图形中的MST中。
在以下的算法中,我们在不同的子图上找到MST,在此过程中,会不断地丢弃不属于全局MST(global MST)的边。一旦到达可以将剩余的边存储在一台机器上的阶段,就可以使用Kruskal算法的单机器版本来计算最终的MST。
5.1 边分割(Edge Partitioning)
单台计算机的内存无法存储下原图中所有的边,那我们就把边分配给计算机集群,每台计算机上的边构成一个子图。在每台计算机上使用Kruskal算法的单机版本计算最小生成树,把这些最小生成树的边集合起来,再次分配给计算机集群,以此反复,直至所有的边减少到能够放入一台计算机上。我们就把它们收集在一台计算机上,并使用Kruskal算法计算最终的MST。

5.1.1 分析
我们使用下面的符号来进行分析:
顶点的数量:n
边的数量:$m = n^{1 + c}$
每台机器上的内存(每台机器上分配的边的数量):$\eta = n^{1 + \epsilon}$
需要机器的数量:$l = \frac{m}{\eta} = n^{c - \epsilon}$
引理5.2 算法将会进行$\left\lceil \frac{c}{\epsilon}\right\rceil$轮迭代后终止,并返回最小生成树。
证明 $\left\lceil \frac{c}{\epsilon} \right\rceil$是向上取整$\frac{c}{\epsilon}$的意思,通过引理5.1我们知道不属于子图最小生成树的边,也不是原图最小生成树的边。既然边的分配的随机的,我们可以预想到每台机器上分配的边数是$\eta$。在第一轮迭代后,我们有$\left| \cup_{i}T_{i} \right| \leq l \times \left( n - 1 \right) = n^{c - \epsilon} \cdot \left( n - 1 \right) = n^{1 + c - \epsilon} + n^{c - \epsilon} = O\left( n^{1 + c - \epsilon} \right)$。因此边的总数变成原来的$\frac{1}{n^{\epsilon}}$。
在下一轮迭代时,如果选择的参数l,恰能够让剩余的边都存储在l台机器上,我们能够证明边的总数再次变为原来的$\frac{1}{n^{\epsilon}}$。因此我们重复这个过程,在$\left\lceil \frac{c}{\epsilon} \right\rceil - 1$轮迭代后,边的数量应该减小到能放入一台机器中运算,整个算法恰好终止在第$\left\lceil \frac{c}{\epsilon} \right\rceil$轮循环
补充
假设一台机器上能分配原图中所有的边,那么经过KRUSKAL算法计算后,会获得最小生成树,根据图论中的定理,$m = n - 1$,但由于每台机器上实际只分配$\eta$数量的边,$\eta \leq m$,所以$\eta \leq n - 1$,$\left| \cup_{i}T_{i} \right| = l \times \eta \leq l \times \left( n - 1 \right)$。
那么在每轮迭代选取的机器数l是固定的吗?下面我们将证明每轮迭代需要根据当前边的总数来选择合适的l,而不是动用全部的机器。
引理5.3最优机器数应该在每轮迭代后减少,需要保证$\frac{\left| e_{i} \right|}{l_{i}}$是常数,恒等于$\frac{m}{l}$。在这里,$e_{i}$是在第$\left( i - 1 \right)^{\text{th}}$轮迭代后剩余的边数,而$l_{i}$是第$i^{\text{th}}$轮迭代后使用的机器数。
证明 让我们假设算法终止于t轮迭代。我们知道在$t -
1$轮迭代后,一台机器的内存可以容纳下剩余的边。因此整个过程的处理时间可以被写成:
$$ \frac{m}{l_{1}}logn + \frac{l_{1}n}{l_{2}}logn + \frac{l_{2}n}{l_{3}}logn + \ldots + \frac{l_{t - 2}n}{l_{t - 1}}logn + l_{t - 1}\text{nlogn} $$
在算法3的第7行,我们将$i -
1$轮迭代剩余的边再次分配给$l_{i}$台机器运算。因为这$l_{i}$台机器是并行运算的,且每台机器上运算的时间复杂度应该是一样的,所以总的处理时间上,只需考虑一台机器的处理时间即可。
KRUSKAL算法的时间复杂度是$O(mlogn)$,m代表边数,n代表顶点数。在引理5.2的证明中,我们有$\left| \cup_{i - 1}T_{i - 1} \right| \leq l_{i - 1} \times \left( n - 1 \right) = O(n^{1 + c - \epsilon}) = O(l_{i - 1} \times n)$,$\left| \cup_{i - 1}T_{i - 1} \right|$就是$i - 1$轮迭代后剩余的边的总数,那么在i轮循环时须将其分配给$l_{i}$台机器,所以这一轮迭代,每台机器上的处理时间为$\frac{\left| \cup_{i - 1}T_{i - 1} \right|}{l_{i}}logn = \frac{l_{i - 1} \cdot n}{l_{i}}\text{logn}$。
想求得最优的$l_{i}$,我们需要
$$ T = \frac{m}{l_{1}}logn + \frac{l_{1}n}{l_{2}}logn + \frac{l_{2}n}{l_{3}}logn + \ldots + \frac{l_{t - 2}n}{l_{t - 1}}logn + l_{t - 1}\text{nlogn} $$
依次对$l_{1},l_{2},\ldots,l_{t - 1}$求偏导,并令其等于零,即
$$ \frac{\partial T}{\partial l_{1}} = 0 $$
$$ \frac{\partial T}{\partial l_{2}} = 0 $$
$$ \vdots $$
$$ \frac{\partial T}{\partial l_{i}} = 0 $$
$$ \vdots $$
$$ \frac{\partial T}{\partial l_{t - 2}} = 0 $$
$$ \frac{\partial T}{\partial l_{t - 1}} = 0 $$
化简后得,
$$ l_{1}^{2} = l_{2}\frac{m}{n} $$
$$ l_{2}^{2} = l_{1}l_{3} $$
$$ l_{3}^{2} = l_{2}l_{4} $$
$$ \vdots $$
$$ l_{i}^{2} = l_{i - 1}l_{i + 1} $$
$$ \vdots $$
$$ l_{t - 2} = l_{t - 3}l_{t - 1} $$
$$ l_{t - 1}^{2} = l_{t - 2} $$
根据引理5.2,令迭代轮次$t = \frac{c}{\epsilon}$,初始条件有$l_{1} =
frac{m}{eta} = n^{c - epsilon}$,代入上面的方程中可得,
$$ l_{1} = n^{c - \epsilon} = \left( \frac{m}{n} \right)^{\frac{t - 1}{t}} $$
$$ l_{2} = n^{c - 2\epsilon} = \left( \frac{m}{n} \right)^{\frac{t - 2}{t}} $$
$$ l_{3} = n^{c - 3\epsilon} = \left( \frac{m}{n} \right)^{\frac{t - 3}{t}} $$
$$ \vdots $$
$$ l_{i} = n^{c - i\epsilon} = \left( \frac{m}{n} \right)^{\frac{t - i}{t}} $$
$$ \vdots $$
$$ l_{t - 1} = n^{c - (t - 1)\epsilon} = \left( \frac{m}{n} \right)^{\frac{1}{t}} $$
所以
$$ \frac{\left| e_{i} \right|}{l_{i}} = \frac{n^{1 + c - \left( i - 1 \right)\epsilon}}{l_{i}} = n^{1 + \epsilon} = constant $$
5.1.2 处理时间和通讯成本
每次迭代的处理时间是在一台机器上执行Kruskal运算所花费的时间(并行的原因),加上为下一次迭代划分剩余边缘所花费的时间。总处理时间可以写成:
$$ \left\lceil \frac{c}{\epsilon} \right\rceil \times \left( O\left( \frac{m}{l}\text{logn} \right) + O\left( \frac{m}{l} \right) \right) $$
通讯成本涉及t个多对多通信(all-to-all communication),这是由于每轮迭代结束时都会随机分配剩余的边。随着边的数量的减少以及迭代的进行,通讯成本也随之降低。总的通信成本是等比数列的求和表达式:
$$ m + \frac{m}{n^{\epsilon}} + \frac{m}{n^{2\epsilon}} + \frac{m}{n^{3\epsilon}} + \ldots + \frac{m}{n^{\left( t - 1 \right)\epsilon}} = \frac{n(n^{c} - 1)}{1 - n^{- \epsilon}} $$
5.1.3 实现
边的随机分配可以通过pyspark的map操作实现。然后,使用groupByKey将具有相同Key的边分配到一台机器上。接下来,flatMap和Kruskal's算法一起使用,获得一个RDD,该RDD里面包含了该轮迭代后剩余的边。
5.2 顶点分割(Vertex Partitioning)
在该算法中,我们不分割边,而是分割顶点。我们固定一个数k并将顶点随机分成k个相等大小的分区,即$V = V_{1} \cup V_{2} \cup V_{3} \cup \ldots \cup V_{k}$且对于$i \neq j,V_{i} \cap V_{j} = \varnothing$。因此$\left| V_{i} \right| = \frac{n}{k}$。如果我们只计算这些分区的构成的子图的最小生成树,那我们会忽略跨越分区的边。所以,我们需要以成对的方式考虑,这样才不会遗漏边。对于每一对分区$i,j$,令$E_{i,j} \subseteq E$表示这些分区顶点$V_{i} \cup V_{j}$所产生的边。即$E_{i,j} = \{(u,v) \in E|u,v \in V_{i} \cup V_{j}\}$。那么每一对分区对应的子图可以表示为$G_{i,j} = (V_{i} \cup V_{j},E_{i,j})$。因为有k个分区,两两配对构成一对,每一对对应一个子图,所以总共有$C_{k}^{2}$个子图。对每一个$G_{i,j}$计算唯一的最小生成树$M_{i,j}$。令H表示所有的$M_{i,j}$包含的边构成的图,即$H = (V, \cup_{i,j}M_{i,j})$.
最后,根据假设H能够放入一台机器的内存中,计算H的最小生成树M,则M是原图G的最小生成树。
5.2.1 分析
定理5.4算法计算出的最小生成树M是G的最小生成树
证明
算法顶点分割的方法,实际上是对原图的稀疏化,之后又计算子图的最小生成树。根据引理5.1,显然我们并未移除属于原图G最小生成树的边。因此最终计算的M确实就是原图G的最小生成树。

对于此算法,我们假设我们能够在一台机器上放入$\tilde{O}(n^{1 + \frac{c}{2}})$大小的边集,其中$m = n^{1 + c}$。$\tilde{O}$和$O$是相同的,只是我们忽略了对数项。
引理5.5令$k = n^{\frac{c}{2}}$,则有$E_{i,j}$的大小有很大的概率是$\tilde{O}(n^{1 + \frac{c}{2}})$
证明
我们通过顶点度数的边界来寻找$E_{i,j}$的边界。$G_{i,j}$的边数显然小于等于顶点的度数和,即$\left| E_{i,j} \right| \leq \sum_{v \in V_{i}}^{}{\deg\left( v \right)} + \sum_{v \in V_{j}}^{}{deg(v)}$。为了证明,我们将原图G所有的顶点按照度数分组。$W_{1}$表示度数为1或2的顶点,$W_{2}$表示度数为3或4的顶点,当$i \geq 2$时有$W_{i} = \{ v \in V:2^{i - 1} < \deg\left( v \right) \leq 2^{i}\}$。假设G有n个顶点,则顶点有$\text{logn}$个分组。
考虑从$W_{i}$映射到$V_{j}$中的顶点数。如果$W_{i}$中有较少的元素,那么$\left| W_{i} \right| < 2n^{\frac{c} {2}}\text{logn}$,有$\sum_{v \in V_{i}}^{}{\deg\left( v \right) \leq 2n^{1 + \frac{c}{2}}logn =}\tilde{O}(n^{1 + \frac{c}{2}})$。如果$W_{i}$中有较多的元素,那么$\left| W_{i} \right| > 2n^{\frac{c}{2}}\text{logn}$,根据Chernoff边界界可以知道从$W_{i}$映射到$V_{j}$中的顶点数等于$O(logn)$的概率至少为$1 - \frac{1}{n}$,即
$$ P\lbrack|W_{i} \cap V_{j}| = O(logn)\rbrack \geq 1 - \frac{1}{n} $$
令$X = |W_{i} \cap V_{j}|$,由Chernoff边界可得
$$ E(X) = O(logn) $$
$$ P\left( X > \left( 1 + \delta \right)\text{logn} \right) \leq e^{- \frac{\delta^{2}\text{logn}}{3}} $$
$$ P\left( X > \left( 1 + \delta \right)\text{logn} \right) \leq e^{- \frac{\delta^{2}\text{logn}}{3}} $$
$$ P\left( X > \left( 1 + \delta \right)\text{logn} \right) \leq \frac{1}{n}e^{\frac{\delta^{2}}{3}} $$
当$\delta \rightarrow 0$时
$$ P\left( X > logn \right) \leq \frac{1}{n} $$
$$ P\left( X \leq logn \right) \geq 1 - \frac{1}{n} $$
因此,至少有$1 - \frac{l\text{ogn}}{n}$的概率
$$ \sum_{v \in V_{j}}^{}{\deg\left( v \right) \leq \sum_{i}^{}{\sum_{v \in V_{j} \cap W_{i}}^{}{deg(v)}}} \leq \sum_{i}^{}{2n^{1 + \frac{c}{2}}}\operatorname{}n \leq \tilde{O}(n^{1 + \frac{c}{2}}) $$
证毕。
5.2.2 处理时间和通讯成本
我们使用下面的符号来进行分析:
顶点的数量:n
边的数量:$m = n^{1 + c}$
每台机器上的内存(每台机器上分配的边的数量):$\eta = n^{1 + \frac{c}{2}}$
需要机器的数量:$k = \frac{m}{\eta} = n^{\frac{c}{2}}$
我们前面证明了,每台机器上边的数量有很高的概率是$O(n^{1 + \frac{c}{2}})$,即$O(\frac{m}{k})$。每台机器上点的数量为$O(\frac{n}{k})$。而且,我们知道在一轮迭代后,我们就能够将剩余的$O(n^{1 + \frac{c}{2}})$放在一台机器上。我们使用Kruskal算法就能够算得最小生成树。因此,总处理时间为一台机器上执行Kruskal运算所花费的时间(并行的原因),加上最后一次执行Kruskal所花费的时间:
$$ O\left( \frac{m}{k} \cdot \frac{\text{logn}}{k}\ \right) + O(n^{1 + \frac{c}{2}} \cdot logn) $$
通讯成本涉及一个一对多的广播(one-to-all broadcast),我们需要将点的分配情况广播到所有的$C_{k}^{2}$台机器上。还涉及一个多对多(all-to-all)的groupByKey,因为我们需要将相同Key的边收集到一台机器上。最后,还有一个多对一(all-to-one)的通讯,我们在最后一步收集了所有剩余的边,将其放在一台机器上执行Kruskal算法。因此总通讯成本为:
$$ O\left( nk^{2} \right) + O\left( m \right) + O(n^{1 + \frac{c}{2}}) $$
对于通信时间,我们假设广播是由比特流模型(BitTorrent Model)完成的。最后的多对一收集(all-to-one collect),每一台机器都会发送$n^{1 - \frac{c}{2}}$大小的数据。因此,总通讯成本可以写成:
$$ O\left( n\log k \right) + O\left( m \right) + O(n^{1 - \frac{c}{2}}) $$
注意到为了分析,我们已经假设了$k = n^{\frac{c}{2}}$。倘若我们拥有的机器数少于$n^{\frac{c}{2}}$,令机器数为l,那么处理时间需要乘以因数$\frac{l}{k}$,处理时间可以重写为l的表示式。
5.2.3 实现
使用带有pyspark随机数生成器的map操作将顶点随机分区,然后将其广播到所有机器。接下来,我们遍历机器上的所有边以找出它所属的一对分区$E_{i,j}$。使用flatMap,为每个边分配对应于其一对分区的Key。groupByKey操作收集一台计算机上属于一个分区的所有边,然后我们在每台机器上应用Kruskal算法。由于一条边可以属于多对分区,因此在第一个Kruskal之后,我们需要使用distinct函数来删除重复项。对剩余的边再用一次Kruskal,可以得到最终的最小生成树。
5.3 并行Prim's(Parallel Prim's)
该算法与上述两个算法的不同之处在于,它是从头开始构建最小生成树(MST)而不是消除不属于最小生成树的边。同样,我们假设原始图的边不能放入单个机器的内存,而顶点可以。第一步,我们找到离开每个顶点的最小边。我们将这些边添加到MST,然后在每个后续迭代中,找到保留每个连接组件的最小边,并将它们添加到MST。可以通过以下方式找到离开每个连接的组件的最小边:找到在单个机器上离开每个连接的组件的最小边,然后执行归约运算(reduce
operation)以获取总体上最小的边。

5.3.1 分析
引理5.6 算法至多需要进行$\left\lceil log_2 n \right\rceil$轮迭代后完成
证明
每一步,我们寻找离开每一个连接组件的最小的边。因此,根据握手引理(handshake lemma),在第i轮迭代中找到的唯一边的数量至少为$\frac{z_{i}}{2}$,其中$z_{i}$为在第i轮迭代开始时连接组件的数量。因此在第i轮迭代的最后,最多有$\frac{z_{i}}{2}$个连接组件。如果我们有$\frac{z_{i}}{2}$以上的唯一边,则迭代结束时的连接组件只会更少。
在第一轮迭代开始时,每一个顶点就是一个连接组件,即$z_{1} = n$。因此,第一轮迭代添加的唯一边的数量至少为$\frac{n}{2}$。这意味着,在第一轮迭代结束后,最多有$\frac{n}{2}$个连接组件。
通过归纳,我们可以得知,第i轮迭代结束后,最多有$\frac{n}{2^{i}}$个连接组件。当我们最后只剩下一个连接组件时,我们就找到了最小生成树。因此,该算法的迭代总数为至多为$\left\lceil log_2 n \right\rceil$。
5.3.2 处理时间和通讯成本
每次迭代的处理时间包含了三部分,
- 在每台机器上找到离开每个组件的最小的边所需的时间
- 执行归约操作(reduce operation)获取最小边所需的时间
- 找到需要执行合并操作(union operation)的边所需的时间
如果使用了路径压缩来高效地实现算法,则不相交数据结构的每次操作的成本为$O(\alpha(n))$。由于此函数的增长非常缓慢,大部分情况下是一个小于5的常数。因此,我们可以假定不相交集合的操作花费的时间是恒定的。
引理5.6 中我们已经证明了在i轮迭代后,连接组件最多有$\frac{n}{2^{i}}$个。规约(reduce operation)的总处理时间可以表示成一个等比数列的和,
$$ \frac{\text{nk}}{2} + \frac{\text{nk}}{4} + \frac{\text{nk}}{8} + \ldots + \frac{\text{nk}}{2^{i}} = O(nk) $$
合并操作的总处理时间与规约操作的时间是相同的,因为我们假设了不相交集合的操作时间是一个常数。因此,总处理时间可以写成,
$$ logn \times O\left( \frac{m}{k} \right) + O(nk) $$
在每轮迭代中,我们有一个对不相交数据结构的一对多的广播。这是用类似比特流(BitTorrent-like broadcast)的广播实现的。每轮迭代中不相交子集的数据结构大小是$O(n)$,它会广播到k台机器上。因此,广播的通讯成本为$O(nk \cdot logn)$。由于我们使用类似比特流的广播,故广播的通讯时间为$O(n \cdot logk \cdot logn)$。
我们还有一个多对一的归约操作,来寻找离开每个连接组件的最小边。由于在第i轮迭代的连接组件最多有$\frac{n}{2^{i}}$个,归约操作的通讯成本为
$$ \frac{\text{nk}}{2} + \frac{\text{nk}}{4} + \frac{\text{nk}}{8} + \ldots + \frac{\text{nk}}{2^{i}} = O(nk) $$
而归约是并行进行,所以归约的通讯时间为,
$$ \frac{n}{2} + \frac{n}{4} + \frac{n}{8} + \ldots + \frac{n}{2^{i}} = O(n) $$
因此总的通讯成本 = 广播通讯成本 + 归约通讯成本,即
$$ O\left( nk \cdot logn \right) + O(nk) $$
总通信时间 = 广播通讯时间 + 归约通讯时间,即
$$ O\left( n \cdot logk \cdot logn \right) + O(n) $$
5.3.3 实现
我们可以在pyspark中实现自定义的不相交集合类。但是,为了节省计算资源并避免编写自定义的序列化方法,我们使用哈希表来存储每个顶点所属的不相交集合,然后广播该哈希表。然后,我们可以调用map操作来寻找每台机器上的最小边,并执行规约操作以获取整体的最小边。之后,我们遍历边列表里的每一条边,返回规约和合并后的结果。
6 理论比较
下面这张表里列出了三种分布式算法的处理时间和通讯时间。
| 边分割 | 顶点分割 | 并行Prim's | |
|---|---|---|---|
| 处理时间 | $O\left( \frac{m}{\text{ϵk}}\text{logn} \right)$ | $O\left( \left( \frac{m}{n^{\frac{c}{2}}} + n^{1 + \frac{c}{2}} \right)\text{logn} \right)$ | $O\left( \frac{m}{k}logn + nk \right)$ |
| 通讯时间 | $O\left( m \cdot \frac{1 - n^{- c}}{1 - n^{- \epsilon}} \right)$ | $O\left( m + cnlogn \right)$ | $O\left( nlogk \cdot logn \right)$ |
其中$m = n^{1 + c}$,每台机器的内存(存储的边数)是$n^{1 + \epsilon}$。
下面我们分别做出三种分布式算法的处理时间和通讯时间随c的变化曲线。这里,我们取$epsilon
= frac{c}{5}$
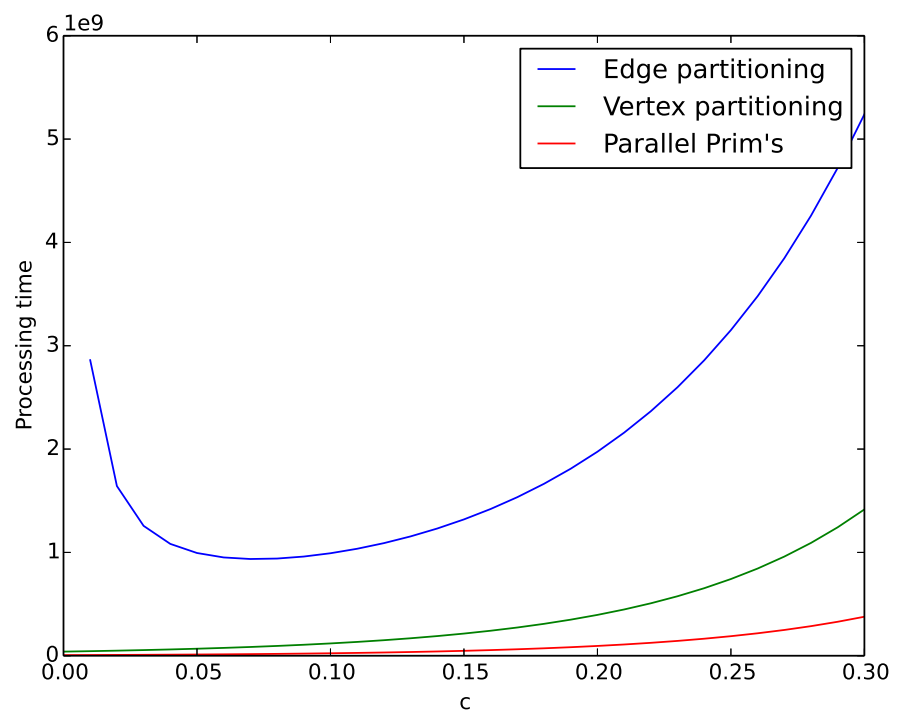
图2 处理时间和c的关系曲线图,$n = 1,000,000$
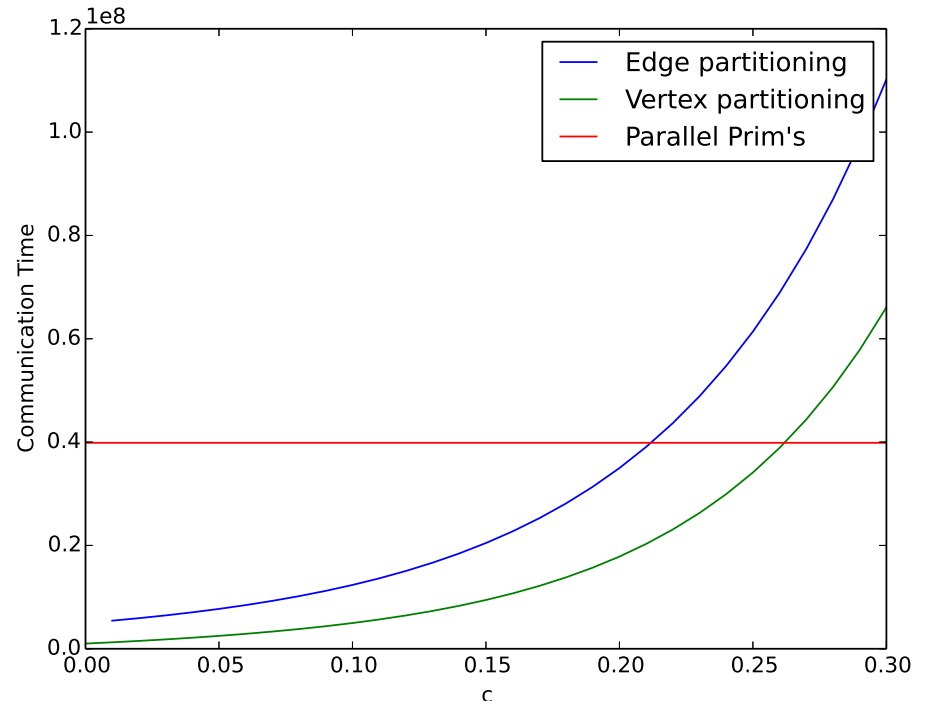
图3通讯时间和c的关系曲线图,$n = 1,000,000$
我们可以看到并行Prim's算法的处理时间更小,且与边分割和顶点分割两种算法相比,增长得更慢。在通讯上,Prim's算法比另外两种算法在稀疏图上需要花费更多的时间,但是随着图的稠密程度的增加,并行Prim's算法在处理时间和通讯时间上都要优于另外两种算法。而且并行Prim's算法的通讯时间与边数没有关系,边数的增加并不会增加它的通讯时间。
7 实验结果
表1 Jure Leskovec and Rok Sosič的实验结果[5]
| 顶点数 | 边数 | 边分割 | 顶点分割 | 并行Prim's | |
|---|---|---|---|---|---|
| web-Stanford | 281,903 | 2,312,497 | 791s | 361s | 92s |
| web-Google | 875,713 | 5,105,039 | 7,384s | 3,733s | 229s |
| web-BerkStan | 685,230 | 7,600,595 | 3,670s | 1,569s | 313s |
| as-Skitter | 1,696,415 | 11,095,298 | >7,200s | >3,600s | 335s |
| roadnet-PA | 1,088,092 | 1,541,898 | >7,200s | >3,600s | 394s |
实验结果符合前面的理论的分析预期,但我们我们注意到的一个反常的现象。尽管as-Skitter的图和roadnet-PA相比有更多的顶点和边,但是它的并行Prim's算法的运行时间却小于roadnet-PA的。这是因为并行Prim's算法运行的迭代次数和图的结构有关。我们前面的分析假设了最糟糕的情况,即至多需要进行$\left\lceil \operatorname{}n \right\rceil$轮迭代,而实际上可能只需更少的迭代次数,这与图的结构有关。
8 结论
- 提出了三种计算给定图的MST的分布式算法,并根据处理时间和通信时间进行了比较。
- 并行Prim算法的通信时间与边数无关。
- 对于稀疏图,顶点分割算法的通信时间少于并行Prim's的通信时间,而Prim's算法的处理时间更好。因此,在某些情况下,顶点分割算法可能会表现更好,因此值得考虑。
- 对于稠密图,并行Prim's算法在通信时间和处理时间上均获胜。
- 在所有情况下,顶点分割和并行Prim的性能均优于边分割算法。
9 未来的工作
- 由于上述所有算法最多都在4个内核上进行了测试,因此我们没有研究算法在实际环境中的扩展能力。根据CPU的速度以及可用的网络带宽的多少,算法的性能可能会有所不同。
- 上面介绍的所有运行时都在预期之中,有时甚至是最坏的情况。实际上,它们取决于图的结构,并且随着我们使用as-Skitter和roadnet-PA看到的图的结构而定,可能会有很大的差异。所以,研究不同类型图上算法的性能是非常有意义的。
- 可能存在进一步改进算法设计的方法。例如,可能存在一种用于边分割和顶点分割的巧妙分割方案。或者,对于并行的Prim's,可能存在一种缓存最小边的方法,从而使每个连接的组件都消除了重复的工作。
引用
- Matei Zaharia, Mosharaf Chowdhury, Michael J Franklin, Scott Shenker, and
Ion Stoica. Spark: cluster computing with working sets. In *Proceedings of
the 2nd USENIX conference on Hot topics in cloud computing*, pages 10–10,
2010. - Reza Zadeh. Discrete mathematics and algorithms.
http://web.stanford.edu/class/cme305/Notes/2.pdf. - Silvio Lattanzi, Benjamin Moseley, Siddharth Suri, and Sergei Vassilvitskii.
Filtering: a method for solving graph problems in mapreduce. In *Proceedings
of the twenty-third annual ACM symposium on Parallelism in algorithms and
architectures*, pages 85–94. ACM, 2011. - Howard Karloff, Siddharth Suri, and Sergei Vassilvitskii. A model of
computation for mapreduce. In *Proceedings of the Twenty-First Annual
ACM-SIAM Symposium on Discrete Algorithms*, pages 938–948. Society for
Industrial and Applied Mathematics, 2010. - Jure Leskovec and Rok Sosič. SNAP: A general purpose network analysis and
graph mining library in C++. http://snap.stanford.edu/snap, June 2014.
本博客文章除特别声明外,均可自由转载与引用,转载请标注原文出处:http://www.yelbee.top/index.php/archives/158/
