1 常见的几种密码体制
公钥密码体制(非对称密码体制):
- RSA
- 背包密码体制(提出两年即被破解)
- Rabin
- NTRU 基于环的公钥密码系统
- ECC 基于椭圆曲线
- SM2
- DSA(Digital Signature Algorithm)
- DH(Diffie-Hellman密钥交换)
私钥密码体制(对称密码体制)
- 流密码:RC4
- 分组密码:DES、RC2、IDEA、3DES、AES、SM4
- 哈希函数:MD5、SHA-1、SHA-2、SM3
2 几个重要的定理
费马小定理
若$p$是素数,$a$是正整数且$gcd(a,p)=1$,则$a^{p-1} \equiv1 \mod{p}$
欧拉函数,设$n$是一正整数,小于$n$且与$n$互素的正整数的个数称为$n$的欧拉函数,记为$\varphi(n)$,
- 若$n$是素数,则$\varphi(n)=n-1$;
- 若$n$是两个素数$p$和$q$的成绩,则$\varphi(n)=\varphi(p) \times \varphi(q)=(p-1)(q-1)$;
- 若$n$有标准分解式$n=p_1^{a_1}p_2^{a_2}\cdots p_t^{a_t}$,则$\varphi(n)=n(1-\frac{1}{p_1})\cdots(1-\frac{1}{p_t})$。
欧拉定理
若 $a$ 和 $n$ 互素,则 $a^{\varphi(n)} \equiv 1 \bmod{n}$
3 RSA
3.1 算法描述
密钥的产生
- 选择两个大素数$p,q$
- 计算$n=p \times q,z=(p-1) \times (q-1)$
- 选取一个整数$e$,满足$1<e<\varphi(n)$,且$gcd(\varphi(n),e)=1$
- 计算$d$,满足$d\cdot e = \equiv 1 \bmod {\varphi(n)}$,即$d$是$e$在模$\varphi(n)$下的乘法逆元,因$e$与$\varphi(n)$互素,由模运算可知,它的乘法逆元一定存在
- 公钥为$\{e,n\}$,密钥为$\{d,n\}$
加密
加密时首先将明文比特串分组,使得每个分组对应的十进制数小于$n$,即分组长度小于$\log_2 n$。然后对每个明文分组$m$,做加密运算$c \equiv m^e \bmod{n}$
解密
对密文分组的解密运算为$m = \equiv c^d \bmod{n}$
证明
...
3.2 RSA的安全性
人类的计算能力的提高和分解算法的不断改进是威胁RSA安全性重要的两个因素。
随着人类计算能力的不断提高....
目前,密钥长度应该介于1024~2048比特之间的RSA是安全的。
需要注意的是,为了保证算法的安全性,$p$和$q$的选取有如下要求:
- $|p-q|$要大
$p-1$和$q-1$都应该要有大素数的因子。
- 这是因为RSA算法存在着可能的重复加密攻击法
3.3 对RSA的攻击
RSA存在以下两种攻击,共模攻击和低指数攻击并不是因为算法本身存在缺陷,而是由于参数选择不当造成的。
共模攻击
实现RSA时,为了方便,我们可能会给每个用户共同的模数$n$,虽然加解密密钥不同,然而这样做是不行的。设两个用户的公钥为$e_1$和$e_2$,且$e_1$和$e_2$互素(一般情况下都成立),明文消息为$m$,密文分别是
$$ c_1 \equiv m^{e_1} \pmod n \\ c_2 \equiv m^{e_2} \pmod n $$
敌手截获$c_1$和$c_2$后,可如下恢复$m$。用推广的Euclid算法求出满足
$$ re_1 + se_2 = 1 $$
的两个整数$r$和$s$,其中一个为负,设为$r$。再次用推广的Euclid算法求出$c_1^{-1}$,由此得$(c_1^{-1})^{-r}c_2^s \equiv m \pmod n$
低指数攻击
假定将RSA算法同时用于多个用户(为讨论方便,以下假定3个),然而每个用户的加密指数(即公钥)都很小。设3个用户的模数分别为$n_i(i=1,2,3)$,当$i \neq j$时,$gcd(n_i,n_j)=1$,否则通过$gcd(n_i,n_j)$有可能得出$n_i$和$n_j$的分解。设明文消息是$m$,密文分别是
$$ c_1 \equiv m^3 \pmod {n_1} \\ c_2 \equiv m^3 \pmod {n_2} \\ c_3 \equiv m^3 \pmod {n_3} $$
由中国剩余定理可求出$m^3 \pmod {n_1n_2n_3}$。由于$m^3 < n_1n_2n_3$,可直接由$m^3$开立方根得到$m$。
4 Diffie-Hellman密钥交换
5 椭圆曲线
什么是椭圆曲线
5.1 椭圆曲线上的运算
无穷远点$O$
无穷远点是椭圆曲线运算的单位元(Identity Element),任何点与$O$相加都会的得到自身,即
$$ O + O = O \\ P + O = P $$
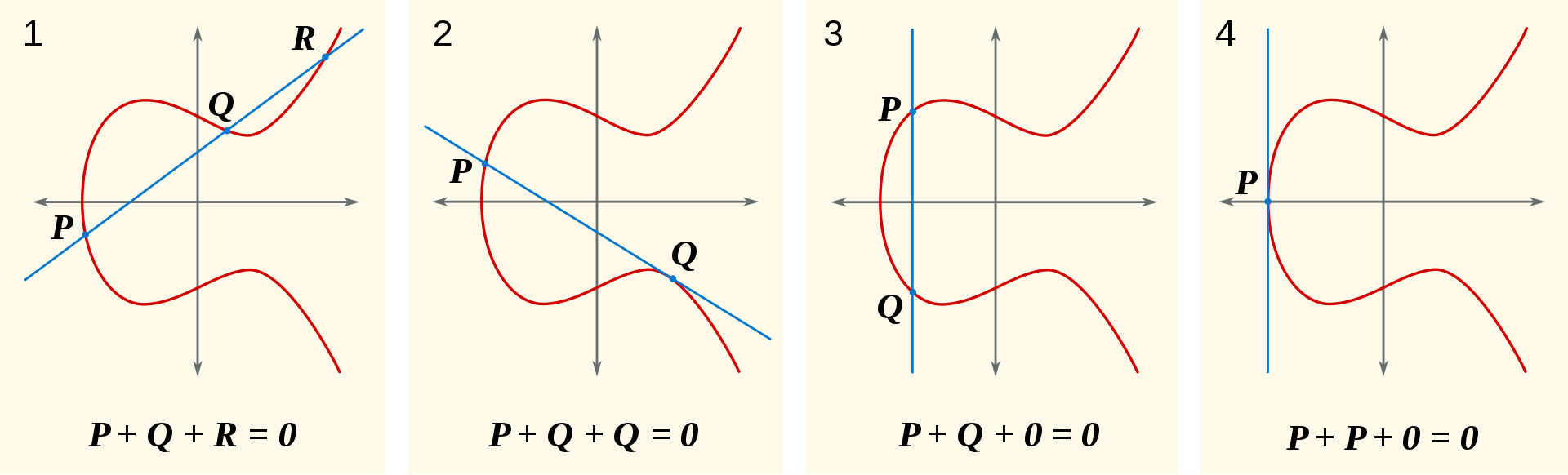
加法运算
图一展示了椭圆曲线上的加法运算是如何进行的,连接$P$和$Q$,交于椭圆曲线的$R$点,然后找关于$x$轴与$R$点对称的点$-R$,即$P+Q=-R$。图二展示了两个相同的点如何运算,我们让图一的$P$点无限地趋近于$Q$点,我们会得到一条经过$Q$的切线,如图二所示,与椭圆曲线交于$P$点,找关于$x$轴对称的点$-R$即为所求,$Q+Q=-P$。图三中的$Q=-P$,$P+(-P)=O$,得到无穷远点$O$,说明连接$P$与$-P$会得到一条垂直于$x$轴的直线,该直线与椭圆曲线在无穷远处相交,这个无穷远处相交就自己想象吧。图四说明两个相同的点相加有可能会得到无穷远点$O$。
多倍点运算
多倍点运算其实就是加法运算的延伸,即$nP$定义为$n$个点$P$相加
$$ nP = P + P + \dots + P $$
- RSA密码体制基于有限域上的大素数的分解问题
- Diffie-Hellmen密钥交换和ElGamal密码体制是基于有限域上的离散对数问题
- ECC椭圆曲线密码体制是基于椭圆曲线上的离散对数问题
考虑方程$Q=kP$,其中$P,Q \in E_p(a,b),k<p$,即$P,Q$是椭圆曲线$E_p(a,b)$上的点,则由$k$和$P$易求得$Q$,但由$Q$、$P$求$k$是困难的,这就是椭圆曲线上的离散对数问题。
5.2 椭圆曲线的签名算法(ECDSA - Elliptic Curve Digital Signature Algorithm)
| Parameter | meaning |
|---|---|
| CURVE | the elliptic curve field and equation used |
| $G$ | elliptic curve base point, a point on the curve that generates a subgroup of large prime order n |
| $n$ | integer order of G, means that $n\times G=O$, where $O$ is the identity element. |
| $d_A$ | the private key (randomly selected) |
| $Q_A$ | the public key (calculated by elliptic curve) |
| m | the message to send |
签名生成
The order $n$ of the base point $G$ must be prime. Indeed, we assume that every nonzero element of the ring $\mathbb{Z} /n\mathbb{Z}$ is invertible, so that $\mathbb {Z} /n\mathbb {Z}$ must be a field. It implies that $n$ must be prime.
Alice creates a key pair, consisting of a private key integer $d_{A}$, randomly selected in the interval $[1,n-1]$; and a public key curve point $Q_{A}=d_{A}\times G$. We use $\times$ to denote elliptic curve point multiplication by a scalar.
For Alice to sign a message $m$, she follows these steps:
- Calculate $e={\textrm {HASH}}(m)$. (Here HASH is a cryptographic hash function, such as SHA-2, with the output converted to an integer.)
Let $z$ be the $L_{n}$ leftmost bits of $e$, where $L_{n}$ is the bit length of the group order $n$. (Note that $z$ can be greater than $n$ but not longer.) - Select a cryptographically secure random integer $k$ from $[1,n-1]$.
- Calculate the curve point $(x_{1},y_{1})=k\times G$.
- Calculate $r=x_{1}\,{\bmod {\,}}n$. If $r=0$, go back to step 3.
- Calculate $s=k^{-1}(z+rd_{A})\,{\bmod {\,}}n$. If $s=0$, go back to step 3.
- The signature is the pair $(r,s)$. (And $(r,-s \mod n)$ is also a valid signature.)
验证签名
For Bob to authenticate Alice's signature, he must have a copy of her public-key curve point $Q_{A}$. Bob can verify $Q_{A}$ is a valid curve point as follows:
- Check that $Q_{A}$ is not equal to the identity element $O$, and its coordinates are otherwise valid
- Check that $Q_{A}$ lies on the curve
- Check that $n\times Q_{A}=O$
After that, Bob follows these steps:
- Verify that $r$ and $s$ are integers in $[1,n-1]$. If not, the signature is invalid.
- Calculate $e={\textrm {HASH}}(m)$, where HASH is the same function used in the signature generation.
- Let $z$ be the $L_{n}$ leftmost bits of $e$.
- Calculate $u_1=zs^{-1} \bmod n$ and $u_2=rs^{-1}\,{\bmod {\,}}n$
- Calculate the curve point $(x_{1},y_{1})=u_{1}\times G+u_{2}\times Q_{A}$. If $(x_1,y_1)=O$ then the signature is invalid.
- The signature is valid if $r\equiv x_{1}{\pmod {n}}$, invalid otherwise.
Note that an efficient implementation would compute inverse $s^{-1}\bmod n$ only once. Also, using Shamir's trick, a sum of two scalar multiplications $u_{1}\times G+u_{2}\times Q_{A}$ can be calculated faster than two scalar multiplications done independently.
证明
It is not immediately obvious why verification even functions correctly. To see why, denote as $C$ the curve point computed in step 5 of verification,
$C=u_{1}\times G+u_{2}\times Q_{A}$
From the definition of the public key as $Q_{A}=d_{A}\times G$,
$C=u_{1}\times G+u_{2}d_{A}\times G$
Because elliptic curve scalar multiplication distributes over addition,
$C=(u_{1}+u_{2}d_{A})\times G$
Expanding the definition of $u_{1}$ and $u_{2}$ from verification step 4,
$C=(zs^{-1}+rd_{A}s^{-1})\times G$
Collecting the common term $s^{-1}$,
$C=(z+rd_{A})s^{-1}\times G$
Expanding the definition of $s$ from signature generation step 5,
$C=(z+rd_{A})(z+rd_{A})^{-1}(k^{-1})^{-1}\times G$
Since the inverse of an inverse is the original element, and the product of an element's inverse and the element is the identity, we are left with
$C=k\times G$
From the definition of $r$, this is verification step 6.
This shows only that a correctly signed message will verify correctly; many other properties are required for a secure signature algorithm.
5.3 椭圆曲线的优点
与基于有限域上的离散对数问题的公钥体制(如Diffie-Hellman密钥交换和ElGamal密码体制)相比,椭圆曲线密码体制有以下优点:
- 安全性高
- 密钥量小
- 灵活性好。有限域GF(q)一定的情况下
椭圆曲线具有丰富的群结构和多选择性,并可在保持和RSA/DSA体制同样安全性能的前提下大大缩短密钥长度(目前160比特足以保证安全性),因而在密码领域有这广阔的应用前景。下表给出了ECC和RSA/DSA在保持同等安全的条件下所需的密钥长度(单位为比特)。
| RSA/SDA | 512 | 768 | 1024 | 2048 | 21000 |
| ECC | 106 | 132 | 160 | 211 | 600 |
6 密钥分发(Key Distribution)
| 密码体制 | 存在的问题 | 解决方案 |
|---|---|---|
| 公钥密码体制 | 两个实体间如何通过不信任的网络建立共享密钥的通道 | 通过可信任的密钥分发中心(KDC - Key Distributed Center)建立密钥交换信道 |
| 私钥密码体制 | 当Alice想获取Bob的公钥,如何能保证得到的一定是Bob的公钥而不是假的呢 | 通过可信任的证书颁发机构(CA - Certification Authority) |
6.1 中间人攻击
6.2 KDC与CA
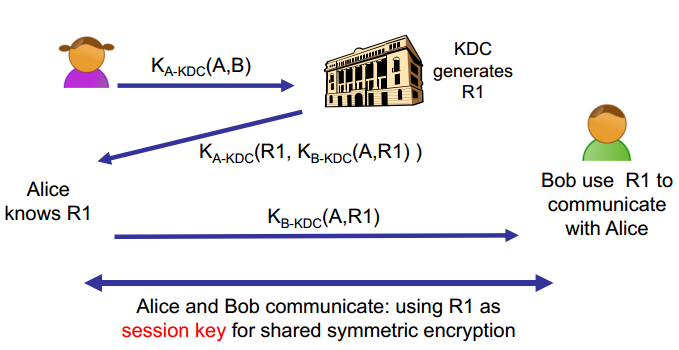
KDC里面会保存每个人的私钥,即一对相同的钥匙,一把在人的手里,另一把在KDC手里,当Alice想和Bob通信时,Alice用和KDC通信的密钥加密请求 (Alice, Bob),KDC收到请求后会随机产生一个R1与A的身份信息放在一起,用和Bob通信的密钥加密这段信息,这样Bob就能确认是Alice想和自己通信,并且大家都使用KDC生成的R1来加解密信息。
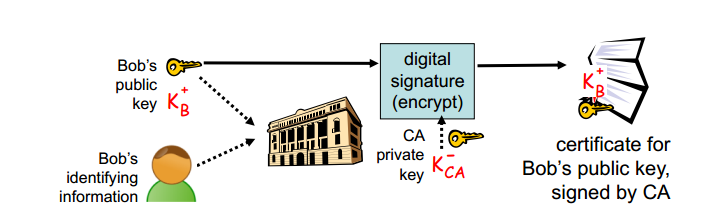
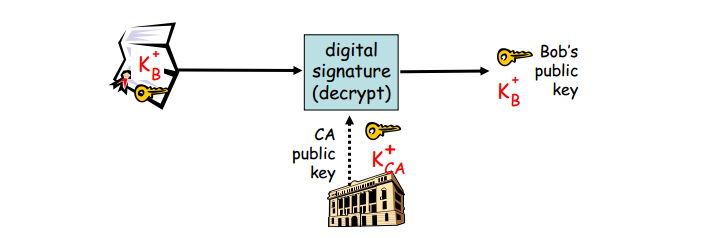
Bob将公钥提供给CA,然后CA使用自己的私钥$K_{CA}^-$加密Bob的公钥$K_B^+$,生成签名后的公钥;而Alice要想获得Bob的公钥则需要使用CA公钥$K_{CA}^+$解密Bob签名后的公钥,得到Bob的原始公钥。

大佬,我是安全猎头云鹤,很高兴通过微博认识一个更加完整的候选人
我们最近帮助很多公司寻找安全人才,其中有一个职位,侧重在安卓加固,有时间微信么